
This is going to be an unusual Papers We Love talk, as I'm going to discuss a bunch of different papers in relatively light detail but with rich historical context. I'll post a transcript and mini-site for this talk that has links to all these papers, and many others that serve as supporting material.
Last year, I gave a talk at Strange Loop where I said everyone is programming wrong. This upset some people, so I thought I'd make a more modest claim today:

We'll need some background to make sense of what follows, so let's start with an easy question...

There are many lenses for this, but I'm going to supply one to serve for the duration of this talk. I think we both invent and discover maths, and part of what we discover is the nature of our own evolved capabilities.

We'll start with geometry, which is the basis for everything else we have.

From this half billion year old bug-like Cambrian swimmer, to bug-eating early mammal, to bug-eating prosimian — given our family tree, it's no surprise our software is full of bugs.
But we all have something else in common, which is that we survive by moving through 3D space. And to move through space, you need to be able to plan based on what you're sensing, which requires you to emulate the world to make predictions about future states.

This is Simone Biles, one of the greatest gymnasts ever to compete. She's showing truly elite human spatial (and thus geometric) ability.
My contention is that everything we do in technical mathematics — the kind we use in engineering and most physics — comes from the same evolved capacities that allow her to plan and execute this elaborate series of translations and rotations.
And our ability to turn those physical gifts inward has given us...

... sculpture and perspective drawing, as well as mathematical geometry.
And our ability to reason about objects in space leads naturally to our...

Many animals have been shown to count objects and work with sequences. This seems to be a natural development of pattern matching and interacting with objects in the world.

Most of you know that pigeons and rats can learn to press a lever a certain number of times to get a treat.
What might be more surprising is that that red forest ants can count to ~20 and communicate those quantities to other ants!
And some animals can apply short term memory...

... to sequences better than most humans. For example, the average chimp handily outperforms the average human at this task.

While number sense exists to some extent in most animals, and geometric sense probably exists in all complex lifeforms, algebra is more specifically human.
It has biological roots in...

This is the first paper I'll recommend today, despite it being about neither computer science nor mathematics. It's an especially good follow up to the bias literature from Kahneman and Tversky.
As a group-living species, our reasoning abilities arose in the context of deliberation, which gave rise to persuasion and the skeptical evaluation of claims. The arms race between these facilities reified cause and effect reasoning into a conscious, reflective, linguistic process. Formal logic and symbolic fluency seem to be downstream of this.
Once we translated the ability to communicate via streams of words into symbols — that is to say, into art and writing — we were able to develop notation, at which point we move from biology to culture.
And one of our most successful cultural artifacts is mathematical notation. So we might ask...

The simplicity and clarity of a good notation not only allows us to serialize our understanding and transmit it to other human beings, it also becomes an engine for our own thinking. In the context of physics and engineering, we really want that notation to speak as directly as possible to our inner gymnast so we can bring our deepest evolved powers to bear on whatever problem we're solving.

As Russel put it, a good notation can act as a teacher, where you bounce your ideas off a formalism that guides you to deeper understanding.
That said, if he were alive today I think he'd go further and champion machine-readable notation — that is to say, programming languages. Anyone here who has both worked through an algebraic problem on paper and also used an interactive programming environment like Mathematica will be able to attest to the power of the latter for improving understanding, so...

I'm going to talk about the history of mathematics in an eccentric way, including anachronistically using programming language metaphors because I think we should remodel our own mathematical practices to take advantage of what we've learnt from programming languages in the 20th century.

I don't have time today to make that argument in full, but I highly recommend this paper I love by Sussman and Wisdom, which discusses work they did creating a scheme-based curriculum for Classical Mechanics. If you'd prefer it in talk form, check out Sussman's Programming for the Expression of Ideas and Sam Ritchie's talks about Emmy — a Clojure port of Sussman's system.

So what properties do we want for this kind of notation?
Okay, let's build a protocol for arithmetic in the same order our cultural ancestors did, starting with...

I say non-negative, but a fun fact about the natural numbers is that there's still no agreement as to whether they include zero.
These are the numbers that we use in informal or folk mathematics, the ones we share with those forest ants...

They're very tangible and intuitive. You can do the first three operations here with any kind of object.
Division is a bit weird though. You either have to accept that the operation returns a tuple of quotient and remainder, which initially feels like a type error, or you need to invent fractions, at which point you have...

... the positive rationals. Whole numbers and vulgar fractions.
Note that these are usually presented after the integers for set theoretical reasons, but we're working in the order they're discovered by each culture.

Once we have the rationals, we have a protocol like this. We first see it at use in ancient Mesopotamia...

N.B. If you're interested in this topic, check out Denise Schmandt-Besserat's research page. She is the person most responsible for our knowledge of this period.
These objects are almost 6000 years old.
The thing at the top is a bulla, which is a kind of spherical clay envelope. The smaller things below are stylized representations of trade goods. Let's say the middle row are croissant tokens. I might put three of them in a bulla, seal it with my amazing cryptographically secure cylinder seal of people walking to the left, and then you could drop by my bakery later to collect your pastries.
This is tangible computing in an extreme sense.
Over time they switched to using tokens to make impressions in clay tablets, so you could just push the goat token down on the tablet five times to indicate five goats.
Then they moved to just drawing directly on the clay with tally marks to indicate quantity.
Fun things to note here: sculpture preceded writing, our first forms of writing were about numbers, and accounting and credit long precede the invention of money.
Anyway, these were very intelligent people, so they quickly invented a more abstract numerical notation...

... that looked like this.
It's base-60, unlike our base-10 numbers, but they had a true place-value system, like our modern one and unlike, say, Roman numerals.

60 is a great base for working with fractions because it has loads of factors. This was important because they did everything with fractions — even their method of division was multiplication by reciprocals, which is to say, for example, that to divide something by two they would multiply it by one half.
To calculate quickly, they used big pre-computed tables of reciprocals, squares, cubes, various roots, and so on. Working engineers used books of precomputed values in this way into the 20th century, right up until computers took over.

I call this tablet a paper I love, but it's actually a 4000 year old homework assignment using Pythagoras's theorem (which you'll note is named after someone born ~1500 years later). The cuneiform writing in the middle shows the square root of 2 to 6 decimal places. They were iteratively approximating irrational numbers in Babylon!
They developed these tools for surveying (calculating areas of parcels in fields) and astronomy (aligning their lunar calendar with the solar one to predict seasons), but they went way further than was reasonable. It's pretty clear the scribal class was composed of the same kind of curious weirdos who invent everything in every other culture.
They solved quadratic and cubic equations, worked with exponential growth and interest rates, and even came up with a form of Fourier analysis to compute the ephemeris. Approximately on par with European mathematics ~3500 years later.
So you might wonder...

They were prosperous and so close to inventing modern technical mathematics. To put it in perspective, we're currently around 600 years after European mathematics reached this point.
The answer, as it so often is...

The agricultural technology that allowed them to feed their big cities and develop their sophisticated culture was unsustainable. Soil grew depleted and salty, gradually reducing crop yields. Then came an interval of rapid climate change that led to famine and war.
Any resemblance to the current era is — I'm sure — entirely coincidental, and no cause for alarm.
Anyway, after around 1550BCE there's a dramatic fall off in mathematical tablets, after which we don't see much progress for nearly 1000 years.
What followed was...

Greeks invented formal proofs ~600BCE, and a couple of people come up with good ways to approximate the area under a curve1, 2, but otherwise not much progress was happening.
One of the reasons for this stagnation was that...

... although Babylonians and Egyptians were okay with approximating irrational numbers, like the sqrt(2), the Greeks thought they were an abomination.
If contemporary accounts are to be believed, people were murdered in Ancient Greece for talking about these numbers, which violated closely held philosophical ideas. Ultimately, they wanted mathematics to be the kind of counting-with-tokens thing we saw earlier, which I contend held them back for reasons that will soon become clear.
Anyway, for the next 1000 or so years various cultures took turns shepherding the surviving wisdom of the ancients. Greeks and Persians, Indian mathematicians, the House of Wisdom in Baghdad. Brahmagupta and Al-Khwarizmi were as important to what we have today as Descartes and Gauss, but in the interest of time we're going skip forward to Italy in the 1500s.

Our protocol has, by this time, grown to include a few more types. We have zero, along with negative and irrational numbers. Some of these "numbers" are a bit strange, but if you squint hard enough you can still mostly pretend that they're at least the same kind of thing as the naturals.
Because we're interested in geometry, let's look at these numbers through a spatial or geometric lens.
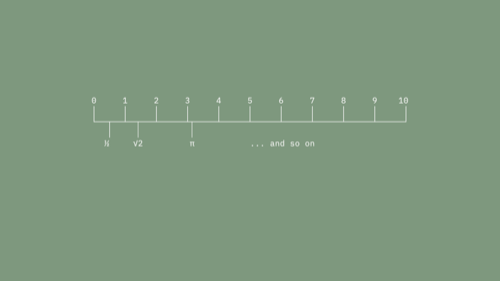
Spatially, this number line is a bit odd. We have an infinite number line, but somehow it also has an end at 0 that serves as a singularity beyond which subtraction fails. Things get more interesting when you add...

To be clear, everybody hated them too, because it's intuitively obvious that you can't have -3 goats. Diophantus said any negative solution to an equation was automatically false. Leibniz hated them. They didn't start to be widely accepted until the mid-19th century!
I think negative numbers are more radical than the irrationals. They change the spatial interpretation of the number line in an important way.
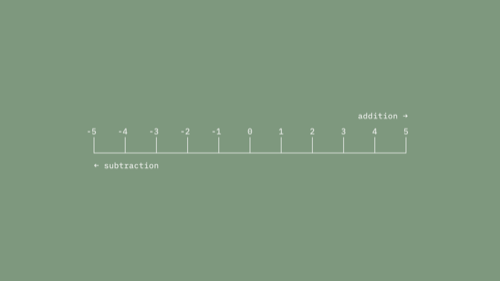
We have the origin at the middle with an infinite extent to either side. It's symmetrical now. So now we can think of addition and subtraction as translation of a point in this infinite space.
And more interestingly...
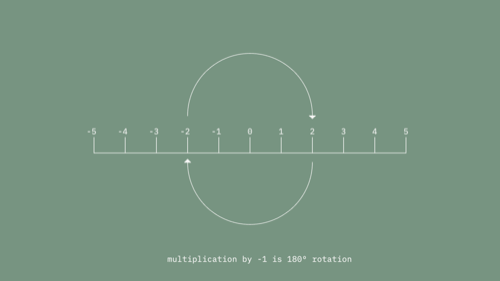
We can interpret the sign flip we get with multiplication by -1 as a rotation around the origin by 180º (or as a reflection, but we're going to focus on rotation here). By adding a new kind of number we get a new kind of space that allows both translation and a limited form of rotation.
The next big discovery, which many of you can already guess, was...
In the 1500s, Rafael Bombelli was trying to deal with an equation of this form...
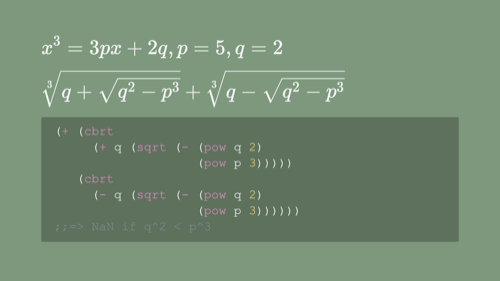
... the solution for which he had gotten from Cardano. This is the algorithm they used to solve cubics at the time, as maths notation and code.
You can see the problem straight away: there's a boundary condition where p3 is greater than q2 after which one needs to take the square root of a negative number. In modern programming terms, this function returns NaN for those cases.

But Bombelli graphed the two components and visually confirmed that they converge. And he was primarily an engineer, so he did what any engineer would do: he kludged it. He used a placeholder with special behavior in these situations, following in the footsteps of Cardano, who invented this approach but thought it useless.
Bombelli wrote a book that included the textual description you see in this block, minus the notation with i, which was retro-fitted in the edition I screen cap'd.

Although I've read them, I'm not recommending any books from this period. They predate anything like modern notation, so the exposition is like this — walls of text mixed with drawings.
Although Bombelli's method worked, everybody hated it...
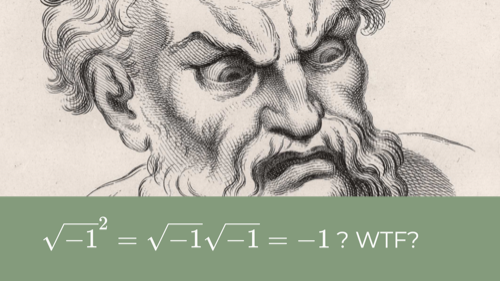
... especially because it seemed to violate existing rules for multiplication. And it just looks a bit arbitrary and magical from the perspective of the time, which was still under Greek influence.
You already know i stand for imaginary, but keep in mind that Descartes coined the term "imaginary number" as an insult to the very idea that such a thing could exist.
But over the next 250 years, because they simplified calculations involving trig, they gained ground. And by the early 1800s...
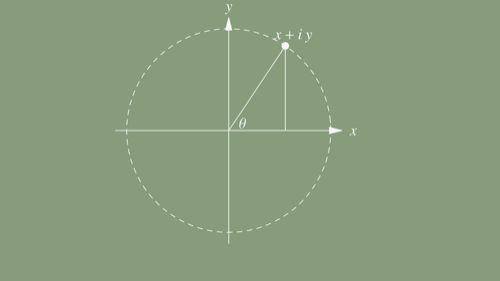
Argand, Gauss, and Wessel independently figured out that they're special geometric numbers that encode rotations in a 2D plane — which, in fairness, was a concept that didn't exist in Bombelli's time.
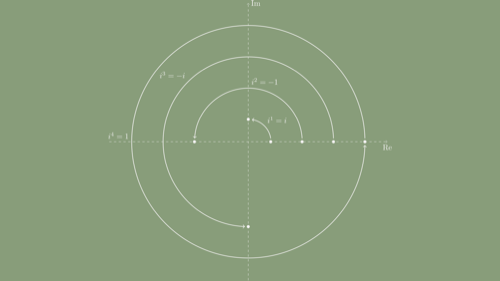
Some find this easier to see looking at an illustration showing that with each exponentiation i rotates 90º. Notice how this feels relative to rotation and sign flip in the positive and negative numbers we saw earlier.
Complex numbers represent the biggest jump toward geometric objects we've seen yet. At this stage it gets very hard to pretend these are numbers in the everyday sense. I think this is inevitable. In order to enlist the gymnastics and perspective drawing part of our brain we had to invent multidimensional objects.
We're now up to the mid-1800s. They were what you might call...

The study of what we now call electromagnetism was heating up, and commercial applications were becoming economically important. The internet boom of the day was...

The telegraph came into commercial use by 1840 and submarine telegraph cables were operating by 1850, allowed rapid communication between continents for the first time.

To put this in perspective, it took two and a half months for a letter to get from London to Sydney! The social and economic impact was tremendous, and we're still living through that accelerando.
This is how electrical engineering began. Our computers descend directly from the telegraph and telephone. Claude Shannon's masters thesis — written around 80 years later — laid the blueprint for digital computers by applying Boolean algebra to analog relays in the telephone system.
The people who were working on these problems at the time were...

Almost all mathematicians were physicists and vice versa.
The big problem they faced was coming up with a system for calculations involving 3D space, including rotations. This was especially important for representing the ideas contained in Maxwell's Equations.
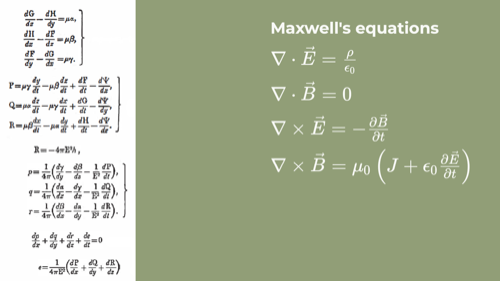
The block on the left is what Maxwell actually wrote. The equations on the right encode the same information using the Gibbs/Heaviside system, which is what's taught today. Even if you can't read it, you can recognize that what's on the right is considerably more concise.
The notational system I prefer captures the same relationships like...
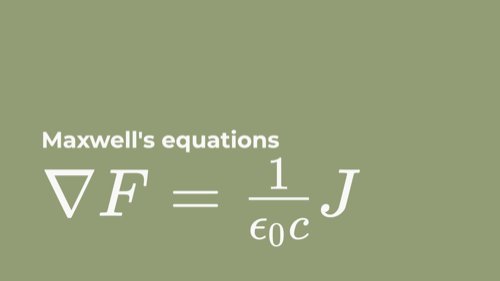
... this:
I'll link to an explanation of the reduction that includes all the details, but for this audience I'd like to just give a very gentle introduction to the notation — Geometric Algebra.

These are Hermann Grassmann and William Clifford.
Grassmann was a German high school teacher who invented most of vector algebra as a side quest while studying tidal theory in his spare time. Unfortunately, his writing was as muddy as his ideas were brilliant, so his work made little impact during his lifetime.
Clifford was an English mathematician and astronomer, and one of the few to read and understand Grassmann's work, which he combined with Hamilton's Quaternions. Clifford called the resulting system Geometric Algebra, though many call it Clifford Algebra in his honor.
Unfortunately, Clifford died of tuberculosis at 33. I suspect we'd have standardized on his approach if he had lived to make the case for it over the following decades.
To talk about this system we add a new kind of mathematical object and three operations to our protocol.


A vector is a geometric object — definitely not a number — that represents a length and a direction. We often call the vector's length "magnitude" (fancy Latin for "bigness").
We're going to cover the basic idea in 2D because that's easier.

Here we have two arrows, one whose positive extent extends to the right called e1 and one that extends upward called e2. These are orthogonal basis vectors of unit length or magnitude of 1.
Note that they're written e1 and e2, not x and y.
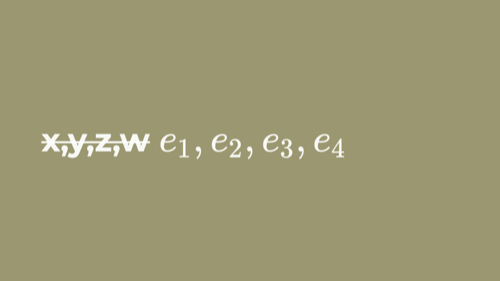
As programmers, when we see ourselves giving individual names to an ordered sequence of similar things, we start to think... maybe this should be an array with indices or something? In that spirit we're using e1, e2, e3, and so on.

We can define an arrow of any length and direction as a linear combination of these basis vectors.
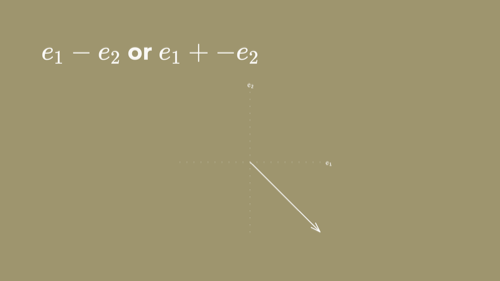
If we subtract e2 from e1, the arrow becomes a downward diagonal. The sign flip inverts the direction of e2, just as it did on the positive/negative number line we saw earlier.
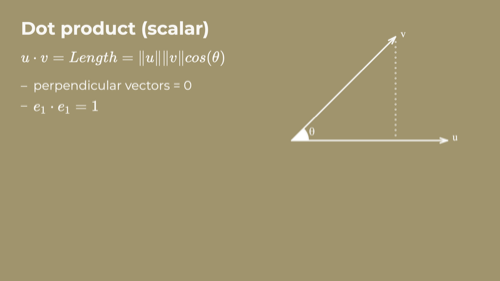
The dot product computes a scalar representing the shared extent of the two vectors, which is the cosine of the angle between them if they've been normed. This is the dot product many of you remember from linear algebra.

The wedge product of these basis vectors returns a bivector. In the same way that vectors represent a directed line, bivectors represent an oriented area, which is a 2D version of a vector's role as a directed magnitude. The direction of the connection of the arrows implies a direction of rotation, as shown here.
In the context of physical calculations, bivectors provide a natural representation for oriented angle of rotation, torque, angular momentum, and the electromagnetic field.
The wedge product is a generalization of vector algebra's cross product that returns a bivector instead of a vector. This ends up making way more sense in most physics calculations.
And the most important one...

Which combines the dot and wedge product. This might look funny because we're adding the scalar from the dot product with the bivector from the wedge product, but we've actually seen this a few minutes ago...

... in the complex numbers. It turns out that the imaginary number i was the unit bivector all along. What was once an algebraic ghost turns out to be a consequence of geometry. I'll link to supporting materials below — the algebraic expansion is quite beautiful!

Okay, let's take a moment to compare two ways of rotating things in 2D. In linear algebra class we're often taught a matrix-oriented approach. To me, that reduces vectors to tuples with benefits. We end up plucking out coefficients and manually grinding them through matrix ops that have limited geometric transparency.
In GA, a vector can almost always be treated as a geometric object that supports our set of operations. And because of how the geometric product works, multiplying a vector by a bivector returns that vector scaled and rotated by the bivector!
The move from matrices to GA feels like going from imperative programming to functional programming.

For a more rigorous treatment of this, and much more besides, I recommend Imaginary Numbers are not Real by Gull, Lasenby, and Doran. These physicist have done loads of work over the last 20 years to popularize GA and their writing is quite accessible.

I've used 2D GA for explanatory purposes, but one of the great strengths of GA is that it generalizes over higher dimensions. Let's take a quick look at the 3D case.
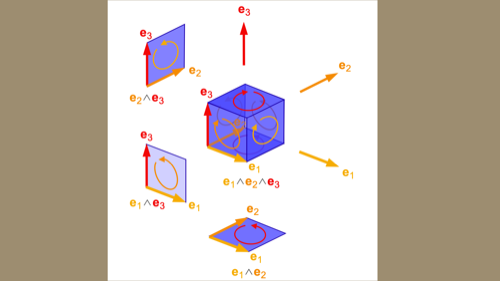
In much the same way that a bivector is a made by wedging together two vectors, a trivector is made by wedging together three bivectors, which makes it an oriented volume. In fact, you can continue this dimensionality increase to arbitrary k-vectors. All the mental tools and notation continue to work. For example, the same isomorphism that gives you complex numbers in 2D gives you quaternions in 3D.
This is extremely useful in physics. Indeed, variations on geometric algebra have been reinvented many times. For example, the Pauli and Dirac algebras are Geometric Algebras invented by physicists to solve physical problems without even knowing about Clifford’s results...

... and a rather large zoo of concepts that are taught with different notations and semantics can be represented directly in geometric algebra. These arose because the Gibbs/Heaviside vector algebra we ended up with wasn't able to accommodate these concepts.

Being able to operate in however many dimensions you please using the same primitives is already great, but we can add one more thing to further generalize the system.

This a little abstract, as in our framework it's basically meta programming. In normal GA, all dimensions square to -1, like the complex numbers. But we can specify that we want to generate an algebra over a space that has a certain number of dimensions that square to -1, 1 or 0. This allows us to represent an even wider range of specialized tools as instances of GA with the same structure-preserving universally applicable operators. A partial list looks like...
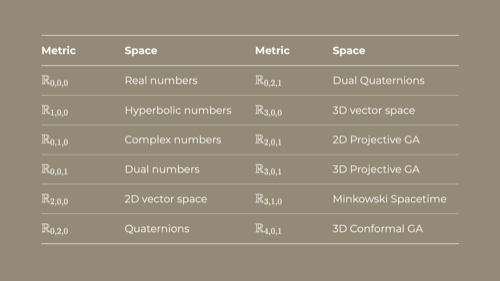
... this. It's not complete, just some commonly useful ones.
It's interesting right away that you can ask for algebras isomorphic to well known geometric objects, like dual numbers and quaternions. This is because these other tools are all special cases of this more general system.
I'll shout out 3D Conformal GA and Minkowski Spacetime. The former makes a number of operations with spheres and circles extremely pleasant, whereas the latter is one of the preferred tools for physicists working with GA because it maps well to relativity.
But today I want to single out Projective Geometric Algebra, which is my favorite for most computer graphics applications.

PGA is great for manipulating points, lines, and planes. It kicked off with robotics research by Selig in 2000, followed by lovely theoretical work by Charles Gunn, but for this audience I'm going to recommend this recent paper by Dorst and De Keninck. You can also find many excellent video presentations and an interactive playground in Javascript called Ganja by De Keninck online. In the meantime, let's do a bit of...

I can't make a presentation for programmers without showing a bit of programming, so...
Physics engine in a few lines of Clojure, hypercubes of various dimension. For an explanation how this works, see Doran and De Keninck's excellent blog post.
Okay, so hopefully this tiny taste has been enough to attract your interest. We're out of time, but before we go, I need to mention...

In the 1960s, Hestenes started work on a research program aimed at refactoring the notation used for technical mathematics using geometric algebra.
My first exposure to these ideas was an 80s paper of his that used geometric algebra to explore zitterbewegung as a lens for understanding the Dirac theory of electrons. It was mind-blowing, and after spending some time with it I came to agree with this quote...

We have a chance here to refactor things in a way that could reduce by maybe 2-3 years the time it takes to educate a young physicist, and in so doing make more advanced topics accessible to many more people. This would, I believe, result in real progress in the sciences, which is why I care enough to bring this to your attention today.

If this talk inspires you to read only one paper, I would ask you to read Hestenes 2002 Oersted Medal Lecture, in which he makes this case very well.

I'll close with this quote from Hestenes old professor, Richard Feynman, and a few thank yous.
First, thanks to Alex Miller for his tireless efforts organizing one of the best technology conferences in the world. And to the organizers of Papers We Love for inviting me.
I'd also like to thank my friend Hamish Todd for telling me over lunch in Berlin a few years ago that an active community had formed around geometric algebra, thus renewing my hopes for the future.
Thanks to my colleagues at Nextjournal for tolerating my eccentricities and supporting my work, including the creation of this talk.
And lastly, of course, thanks to all of you for listening!